Primjer 1.

Izračunati vektor magnetne indukcije u tački A za provodnik na Slici 1. Kroz provodnik teče stalna jednosmjerna struja I, a provodnik se nalazi u vazduhu.

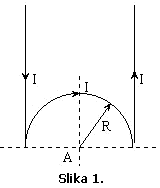
Rješenje:

Vektor magnetne indukcije u tački A koju stvara provodnik sa strujom jačine I sa Slike 1, određuje se superpozicijom vektora magnetnih indukcija koje u tački A stvaraju pojedini dijelovi provodnika kao što je prikazano na Slikama 1.a, 1.b, 1.c. Za svaki od uočenih dijelova provodnika potrebno je odrediti vektore magnetne indukcije.

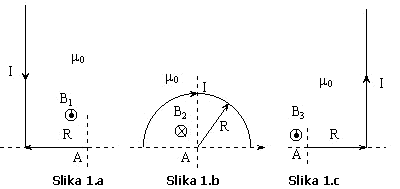
Za provodnik sa Slike 1.a, koristeći izraz i uzimajući da je:

dobija se da je intenzitet magnetne indukcije u tački A:

Provodnik sa Slike 1.b, stvara vektor magnetne indukcije čiji je intenzitet jednak polovini iznosa magnetne indukcije koju stvara kružna kontura u centru.

Analogno određivanju intenziteta magnetne indukcije u tački A na Slici 1.b, određuje se i intenzitet magnetne indukcije u tački A na Slici 1.c, gdje je:

Vektor ukupne magnetne indukcije u tački A određuje se kao suma vektora magnetnih indukcija koje potiču od pojedinih dijelova provodnika:

sa Slika 1.a, 1.b, 1.c može se uočiti da sva tri vektora magnetnih indukcija leže na pravcu koji je normalan na ravan crteža, dok su im smjerovi različiti.

Ako se pretpostavi da je rezultantni vektor magnetne indukcije istog smjera kao i vektori i , tada intenzitet vektora magnetne indukcije u tački A iznosi:

odnosno:

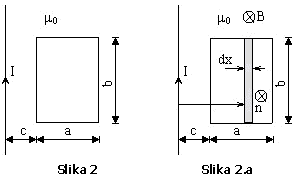
Primjer 2.

Odrediti fluks vektora magnetne indukcije kojeg stvara neograničeno dugi tanki pravolinijski provodnik sa strujom jačine I, kroz pravougaonu konturu prikazanu na Slici 2.

Rješenje:

Intenzitet magnetne indukcije koju stvara neograničeno dugi, tanki, pravolinijski provodnik sa strujom jačine I u nekoj tački na udaljenosti x od ose provodnika iznosi:

Vektor magnetne indukcije je normalan na ravan konture i usmjeren u ravan crteža.

Fluks vektora magnetne indukcije kroz neku površinu S u magnetnom polju jednak je sumi skalarnih proizvoda po površini, gdje označava vektorski element površine S.

Kako su elementi dS male površine one zadovoljavaju uslov da je vektor magnetne indukcije u svim tačkama elemenata dS jednak po intenzitetu i smjeru, tj. da je magnetno polje homogeno.

Fluks vektora magnetne indukcije, uobičajeno se, kraće naziva magnetni fluks, ili samo fluks i predstavlja jednu od najvažnijih veličina u elektrotehnici. Analiza i proračun svih električnih mašina (električnih motora, generatora, transformatora, i dr.) bazirana je na fluksu.

Jedinica za magnetni fluks je . odnosno izvedena jedinica je veber [Wb] prema naučniku Weberu.

Magnetni fluks kroz pravougaonu konturu zavisi od magnetne indukcije uzrokovane proricanjem struje jačine I kroz pravolinijski provodnik i površine posmatrane konture.

Na rastojanju x od provodnika moguće je uočiti elementarnu površinu pravougaone konture dS, Slika 2.a. Vektor elementarne površine dat je izrazom:

Vektor normale leži na pravcu koji je normalan na površinu, a smjer mu se određuje na jedan od slijedećih načina:

- proizvoljno, ukoliko kroz konturu na koju se oslanja površina ne protiče struja,

- ukoliko kroz konturu na koju se oslanja površina protiče struja, smjer se određuje na osnovu pravila desnog zanrtnja u odnosu na smjer struje,

- za zatvorene površine usmjerenje vektora normale na površinu je ka vanjskom prostoru.

U ovom primjeru kroz konturu ne protiče struja, te je smjer vektora normale na površinu odabran u smjeru magnetne indukcije.

Elementarni fluks kroz uočenu elementarnu površinu je:

Ukupni fluks kroz površinu konture je:

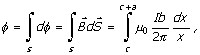
Primjer 3.

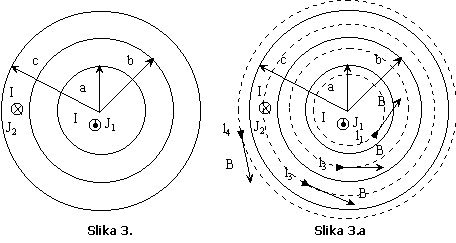
Odrediti magnetnu indukciju koaksijalnog kabla čiji je poprečni presjek prikazan na Slici 3. Smatrati da je struja ravnomjerno raspoređena po poprečnom presjeku pojedinih provodnika kabla.

Rješenje:

Zbog simetrije linije vektora magnetne indukcije su koncentrični krugovi u ravnima normalnim na osu kabla, sa centrima na osi kabla.

Primjenom Amperovog zakona za konturu ima se:

gdje je gustina struje unutrašnjeg provodnika koaksijalnog kabla.

Normala za određivanje fluksa vektora kroz površinu oslonjenu na konturu cirkulacije je pravilom desnog zavrtnja vezana sa usvojenim smjerom cirkulacije po konturi. Odavde je:

za

Za konturu je:

za

Površinska gustina struje u spoljašnjem provodniku koaksijalnog kabla je pa se cirkulacijom vektora magnetne indukcije duž konture dobija:

za

Izvan koaksijalnog kabla za konturu dobije se:

za

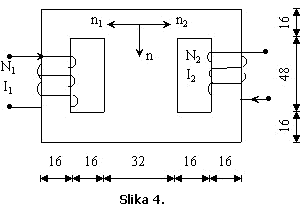
Primjer 4.

Na Slici 4. je prikazano magnetno kolo sa dva namotaja. Kroz prvi namotaj protiče stalna struja jačine . Odrediti jačinu struje koja protiče kroz drugi namotaj tako da u srednjem dijelu magnetnog kola prema naznačenoj normali magnetni fluks bude Debljina feromagnetnog paketa iznosi Karakteristika feromagnetnog materijala data je u tabeli. Magnetno rasipanje zanemariti. Dimenzije magnetnog kola na slici date su u milimetrima.

B[T]	0.08	0.12	0.2	0.4	0.53	0.68	0.8
H[A/m]	25	40	50	65	150	249	950

Rješenje:

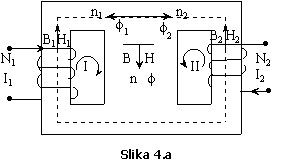
Za dato kolo prema Slici 4. mogu se, prema prvom i drugom Kirchoff-ovom zakonu za magnetna kola, napisati slijedeće jednačine:

(1)

(2)

(3)

Površine poprečnog presjeka i dužina pojedinih dijelova magnetnog kola u kojima djeluje isto magnetno polje iznose:

Na osnovu poznatog magnetnog fluksa moguće je odrediti vrijednost magnetne indukcije B:

Za izračunatu vrijednost magnetne indukcije B iz karakteristike feromagnetnog materijala moguće je utvrditi veličinu magnetnog polja H:

Na osnovu jednačine (2) napisane po drugom Kirhofovom zakonu za magnetna kola, izračunava se veličina magnetnog polja :

Iz tabele za izračunato magnetno polje , određuje se veličina magnetne indukcije

Smjer vektora magnetne indukcije je suprotan u odnosu na vektor normale , tako da se fluks računa kao:

Za poznate magnetne flukseve i moguće je izračunati fluks na osnovu jednačine (1), napisane po prvom Kirchoffovom zakonu za magnetno čvorište:

Magnetna indukcija računa se na osnovu poznatog magnetnog fluksa

Vrijednost magnetnog polja određuje se iz tabele za poznatu magnetnu indukciju .

Jačina struje drugog namotaja , određuje se iz jednačine (3):

Primjer 5.

Odrediti međusobnu induktivnost veoma dugog pravolinijskog provodnika i provodnika u obliku pravougaonika, koji se nalaze u istoj ravni u vazduhu, kao na Slici 5.

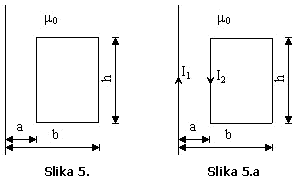
Rješenje:

Međusobna induktivnost pravolinijskog provodnika i provodnika u obliku pravougaonika određuje se na osnovu izraza:

Da bi se odredila međusobna induktivnost potrebno je pretpostaviti struje kroz provodnike. Kroz pravolinijski provodnik je pretpostavljena struja jačine , a kroz pravougaoni provodnik je pretpostavljena struja jačine smjerova kao na Slici 5.a. Struja jačine , predstavlja struju koja protiče kroz pravolinijski provodnik. Ova struja stvara magnetnu indukciju na mjestu pravougaone konture sa smjerom kao na Slici 5.c. Intenzitet magnetne indukcije , jednak je:

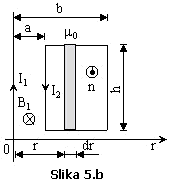
Fluks vektora magnetne indukcije kroz površinu oslonjenu na pravougaonu konturu je:

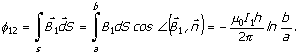
Orijentacija vektora normale na površinu dS, prema Slici 5.b, je određena na osnovu smjera jačine struje kroz pravougaoni provodnik.

Međusobna induktivnost jednaka je:

Primjer 6.

Dati su neograničeno dugi provodnik kroz kojeg protiče struja jačine i pravougaona kontura stranica b i c , sa strujom jačine . Međusobni položaj i dimenzije dati su na Slici 6. Odrediti rad sila elektromagnetnog polja pri pomjeranju konture oko vrha D u ravni konture za ugao u smjeru suprotnom od smjera kretanja kazaljke na satu.

Poznato je:

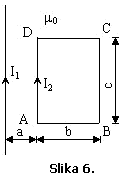
Rješenje:

Rad sila magnetnog polja dat je izrazom:

Fluksevi i predstavljaju flukseve obuhvaćene konturom koja se pomjera pod uticajem sila elektromagnetnog polja provodnika sa strujom jačine , u njenom početnom i krajnjem položaju, respektivno.

Početni položaj konture i veličine za određivanje fluksa dati su na Slici 6.a. Krajnji položaj konture i veličine za određivanje fluksa dati su na Slici 6.b.

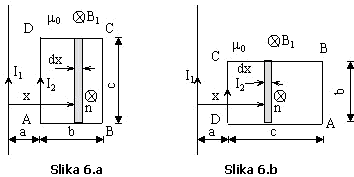
Fluks u početnom položaju dat je izrazom:

Fluks u krajnjem položaju dat je izrazom:

Odavde je rad pri pomjeranju konture za ugao oko vrha D jednak:

Primjer 7.

Odrediti saglasne krajeve za dvije induktivno spregnute zavojnice prikazane na Slici 7.

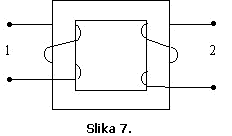
Rješenje:

Postupak za određivanje saglasnih krajeva moguće je opisati na sljedeći način. Za jednu zavojnicu se izabere proizvoljno saglasan kraj u koji struja ulazi svojim pozitivnim smjerom. Prema pravilu desnog zavojka odredi se pozitivan smjer indukovanog fluksa kroz prvu zavojnicu, koji se sa istim smjerom zatvara i kroz drugu zavojnicu. Korištenjem pravila desnog zavrtnja odredi se takav pozitivan smjer struje kroz drugu zavojnicu da indukovani fluks ima isti pozitivan smjer kao i indukovani fluks od prve struje. Kraj druge zavojnice u koji ulazi struja svojim pozitivnim smjerom je saglasan kraj.

Uz pretpostavljeni smjer struje kroz prvu zavojnicu , prethodno objašnjeni postupak prikazan je na Slici 7.a.

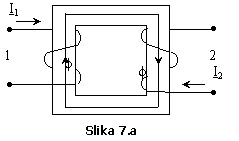
Primjer 8.

Za induktivno spregnuta kola sa različitim izborom saglasnih krajeva na Slici 8. odrediti ekvivalentne sheme.

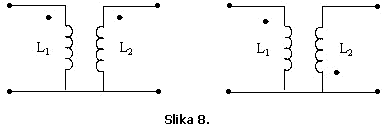
Rješenje:

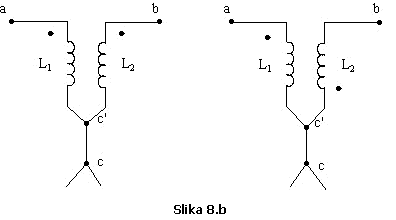
Zbog široke primjene praktična realizacija ekvivalentnih shema će se objasniti nešto detaljnije. Zajednički čvor u koji se stiče po jedan kraj zavojnica i označit će se sa "c", dok su preostala dva kraja označena sa "a" i "b" (Slika 8.a).

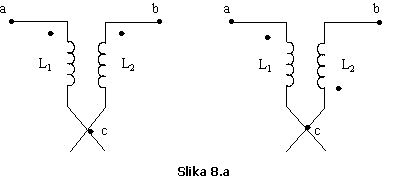
Za realizaciju ekvivalentne sheme neophodno je pored čvora c, formirati i čvor c', za koji je vezan zajednički kraj obje zavojnice i jedna idealno provodna grana koja povezuje čvor c' sa čvorom c za koji i dalje ostaju vezane preostale grane kola (Slika 8.b).

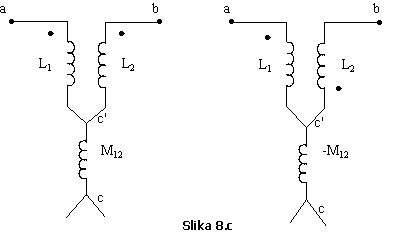
Ekvivaletna shema za jedan i drugi izbor saglasnih krajeva prikazana je na Slici 8.c.

Da bi se odredile vrijednosti pojedinih induktivnih elemenata u ekvivalentnoj shemi razmotriće se slijedeći slučaj.

Neka je kolo za koje je potrebno odrediti ekvivalentnu shemu prikazano na Slici 8.d, a ekvivalentna shema posmatranog kola prikazana na Slici 8.e.

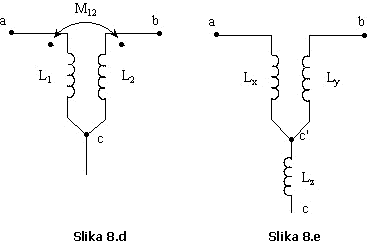
Da bi bio zadovoljen uslov ekvivalencije dva kola sa Slika 8.d i Slika 8.e, potrebno je da ukupna induktivnost između pojedinih čvorova u oba slučaja ostane nepromijenjena:

odnosno:

,

Formiran je sistem od tri jednačine sa tri nepoznate Rješenja razmatranog sistema su:

Na sličan način moguće je izračunati vrijednost induktivnosti u ekvivalentnoj shemi za zavojnice različito odabranih saglasnih krajeva.